Problem Review:
Question: This problem was asked by Uber.
Given an array of integers, return a new array such that each element at index i of the new array is the product of all the numbers in the original array except the one at i.
For example, if our input was [1, 2, 3, 4, 5], the expected output would be [120, 60, 40, 30, 24]. If our input was [3, 2, 1], the expected output would be [2, 3, 6].
Follow-up: what if you can’t use division?
Answer One
Given that division is allowed there is a simple way to achive a solution for this problem using only two loops through the list.
- First Make a temp variable that is initialized to 1 and then iterate through the list multipling the values into temp.
product = 1
for num in listOfNumbers:
product *= num
Warning: Remember to be careful with multiplying by zero
Case: our list is [1,2,0]
We expect the output to be [0,0,2]
However, because we never check for a 0 the output will be [0,0,0]. A case to also consider is any list that has more that a single 0, the product will always be 0.
Because of this a better loop might look like the following.
product = 1
zeros_in_list = 0
for num in listOfNumbers:
if num != 0:
product *= num
else:
#skip multiplying the zero into the product
zeros_in_list += 1
We have a product for all the values in the array, now to get the output array.
- Once we have the product its a simple matter of iterating through the list again and just dividing out the current index.
productList = list()
for num in listOfNumbers:
#case where there are at least 2 zeros
if zeros_in_list > 1:
productList.append(0)
continue
#make sure that we do not divide by 0
if num != 0 and zeros_in_list == 1:
productList.append(0)
elif num == 0:
"""
since this is the case where there is ONLY one 0
once it is found the value at this point is the
product of all the others.
"""
productList.append(product)
else:
#regular numbers are divided out and push into the answer array.
productList.append(product//num)
return productList
This return the list we are looking for, now to look at the follow up question.
Follow-up: what if you cant use dividion?
This is a little harder if we still want to complete this in O(n) time. My solution is using something like a doubly linked list that keeps track of the product of the nodes on its left and right.
Here is an overview of how this can be accomplished.
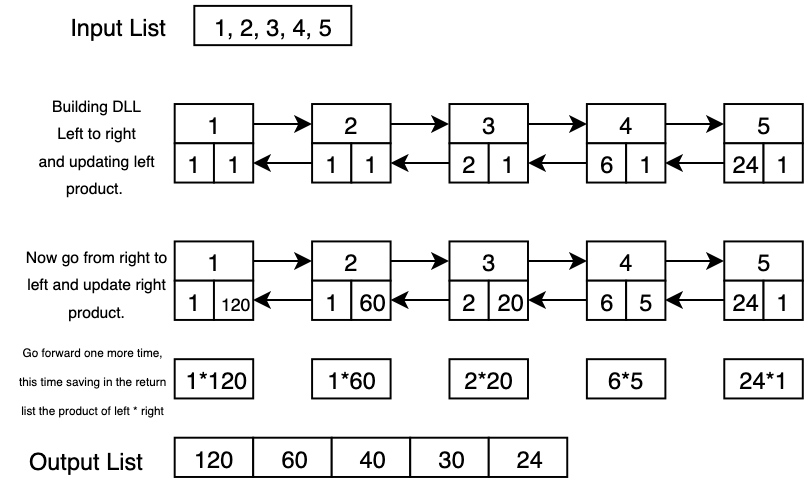
As shown here when you are adding nodes to the list you initialize the product of left and right to 1. When a new node is added you take the previous nodes value and product of the left and multiply them to become the new nodes left product. Once all the nodes have been added iterate backward through the list taking the value of the node to the right and multiplying it by the product of the right.
Once you are back the front of the list we need to go back through once more time but we have to make a new list to save the products we are about to calculate. Take the value of a nodes left product and right product and multiply them together to get what the list of numbers would be without the node you are currently in. Add that new product to the return list and then move to the next node til you find the end of the list.
There are a few ways to do this from a data structure viewpoint, once would be to locally store two lists to add the numbers to as you read them. I opted for a class-based system as shown in the image above. One benefit is that if it was required it would be less time consuming to add new nodes to either the beginning or end of the list. If a new node was added it would only require one pass of the data to update all nodes in the list.
class productListNode(object):
"""docstring for productListNode"""
def __init__(self, value):
super(productListNode, self).__init__()
self.value = value
self.next = None
self.prev = None
self.productOfPrev = 1
self.productOfNext = 1
class productList(object):
"""docstring for productList"""
def __init__(self, startNode = None):
super(productList, self).__init__()
self.head = startNode
self.end = None
def build(self, listOfNumbers):
#forward adding with getting product.
for num in listOfNumbers:
newNode = productListNode(num)
if self.end is not None:
newNode.prev = self.end
self.end.next = newNode
self.end = newNode
else:
self.head = newNode
self.end = newNode
if newNode.prev is not None:
newNode.productOfPrev = newNode.prev.value * newNode.prev.productOfPrev
currentNode = self.end
#now iterate backwards through th elist
while currentNode is not None:
if currentNode.next is not None:
currentNode.productOfNext = currentNode.next.value * currentNode.next.productOfNext
currentNode = currentNode.prev
#ready to get the product list or add new items to the end, this keeps the list up to-date
pass
def print_list_of_products(self):
returnList = list()
currentNode = self.head
while currentNode is not None:
returnList.append(currentNode.productOfPrev * currentNode.productOfNext)
currentNode = currentNode.next
return returnList
pass
Conclusion
- Both answers use a run time complexity of O(n)
- Answer one uses less space than answer two but both require O(n) space, just scaled differently.
- Answer two is insulated against problems with multiplying by zero unlike answer one where we have to check.
If there is a reason you might have to constantly get products from the same list of numbers or a list that keeps having numbers added to it the class based approch might have useful features in it. Overall if you are just looking for a one off process the first approch is much simpler and requires less memory to get the returned list.
If you have any questions feel free to send me a message though my LinkedIn or email provided in the footer.